Rumfang beregner – Beregn rumfanget du skal bruge

Velkommen til en spændende artikel om beregnere til rumfang. Hvis du nogensinde har haft brug for at beregne rumfanget af et objekt, ved du sikkert, hvor tidskrævende og kompliceret det kan være at gøre det manuelt. Men fortvivl ikke! Med de avancerede beregnere til rumfang, som vi vil præsentere i denne artikel, kan du nemt og hurtigt få udregnet rumfanget af enhver form for objekt helt automatisk. Så hvis du vil spare tid og kræfter på at beregne rumfang, er du kommet til det rette sted. Læs videre for at lære mere om disse fantastiske beregningsværktøjer og hvordan de kan hjælpe dig med dine projekter. Husk at alle vores beregnere til rumfang er gratis at bruge, og du kan få resultaterne på et øjeblik.

Det følgende er en liste over rumfangberegnere til flere almindelige former. Udfyld venligst de tilsvarende felter og klik på knappen “Beregn”.

Du kan læse matematikken bag beregningerne i bunden på denne side.

OBS: Husk at alle tal skal skrives i METER (m). Hvis du skal have hjælp til omregningen fra centimeter (cm) til meter (m) så besøg denne side hvor vi har lavet en beregner til netop dette!

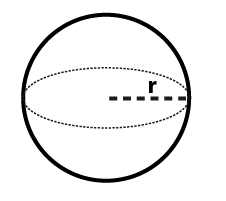
Beregn rumfang af en kugle

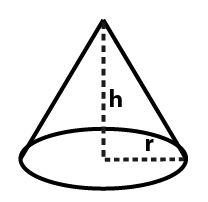
Beregn rumfang af en kegle

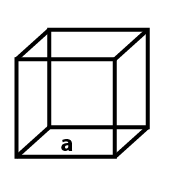
Beregn rumfang af en kvadratisk tank / Terning

Beregn rumfang af en cylinder

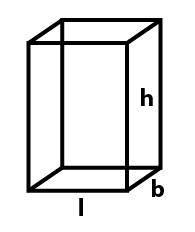
Beregn rumfang af en rektangulær tank

Beregn rumfang af en kapsel

Beregn rumfang af en keglestub

Beregn rumfang af en elipsoide

Beregn rumfang af en pyramide

Beregn rumfang af et rør

Forklaring til hvordan man beregner rumfanget

Rumfanget er kvantificeringen af det tredimensionelle rum et stof optager. SI-enheden for rumfang er kubikmeter eller m3. Ved konvention er rumfanget af en beholder typisk dens kapacitet, og hvor meget væske den er i stand til at rumme, snarere end mængden af plads, som den faktiske beholder fortrænger. Rumfanget af mange former kan beregnes ved at bruge veldefinerede formler. I nogle tilfælde kan mere komplicerede former opdeles i enklere samlede former, og summen af deres volumener bruges til at bestemme det samlede rumfang. Rumfanget af andre endnu mere komplicerede former kan beregnes ved hjælp af integralregning, hvis der findes en formel for formens grænse. Ud over dette kan former, der ikke kan beskrives ved kendte ligninger, estimeres ved hjælp af matematiske metoder, såsom finite element-metoden. Denne lommeregner beregner rumfang for nogle af de mest almindelige simple former.

Rumfang og Volume er det samme. Rumfang bliver blot regnet i m3 mens Volume beregnes i L (Liter) da Volume regnes for væske som oftest bruges vedrørende kemi. Du kan derfor godt bruge vores beregnere selvom du skal beregne en Volumen af en form.

Kugle

En kugle er det tredimensionelle modstykke til en todimensionel cirkel. Det er et perfekt rundt geometrisk objekt, der matematisk set er det sæt af punkter, der er lige langt fra et givet punkt i dets centrum, hvor afstanden mellem midten og ethvert punkt på kuglen er radius r. Det mest almindeligt kendte sfæriske objekt er sandsynligvis en perfekt rund bold. Inden for matematik er der en skelnen mellem en bold og en kugle, hvor en bold omfatter det rum, der er afgrænset af en kugle. Uanset denne skelnen deler en bold og en kugle den samme radius, centrum og diameter, og beregningen af deres rumfang er den samme. Som med en cirkel kaldes det længste linjestykke, der forbinder to punkter i en kugle gennem dens centrum, diameteren, d. Ligningen til beregning af rumfanget af en kugle er angivet nedenfor:

Rumfang af kugle = 4/3 * π * r^3

Kegle

En kegle er en tredimensionel form, der tilspidser jævnt fra sin typisk cirkulære base til et fælles punkt kaldet apex (eller toppunkt). Matematisk er en kegle dannet på samme måde som en cirkel af et sæt linjestykker forbundet til et fælles midtpunkt, bortset fra at midtpunktet ikke er inkluderet i det plan, der indeholder cirklen (eller en anden base). Kun tilfældet med en endelig højre cirkulær kegle behandles på denne side. Kegler bestående af halvlinjer, ikke-cirkulære baser osv., der strækker sig uendeligt, vil ikke blive behandlet. Ligningen for at beregne volumenet af en kegle er som følger:

Rumfang af en kegle = 1/3 * π * r^2 * h

hvor r er radius og h er højden af keglen

Kvadratisk tank / Terning

En terning er den tredimensionelle analog af en firkant og er en genstand afgrænset af seks firkantede flader, hvoraf tre mødes ved hver af dens hjørner, og som alle er vinkelrette på deres respektive tilstødende flader. Terningen er et specialtilfælde af mange klassifikationer af former i geometri, herunder at være en kvadratisk parallelepipedum, en ligesidet kuboid og en højre rombohedron. Nedenfor er ligningen til beregning af rumfanget af en terning:

Rumfang af en terning = a^3

hvor a er terningens sidelængde

Cylinder

En cylinder i sin enkleste form er defineret som overfladen dannet af punkter i en fast afstand fra en given retlinjeakse. I almindelig brug refererer “cylinder” imidlertid til en ret cirkulær cylinder, hvor cylinderens baser er cirkler forbundet gennem deres centre med en akse vinkelret på planerne af dens baser, med en given højde h og radius r. Ligningen til beregning af volumenet af en cylinder er vist nedenfor:

Rumfang af en cylinder = π * r^2 * h

hvor r er radius og h er højden af tanken

Rektangulær tank

En rektangulær tank er en generaliseret form af en terning, hvor siderne kan have varierende længder. Det er afgrænset af seks flader, hvoraf tre mødes ved dets spidser, og som alle er vinkelrette på deres respektive tilstødende flader. Ligningen til at beregne volumenet af et rektangel er vist nedenfor:

Rumfang af rektangulær tank = længe * bredde * højde

Kapsel

En kapsel er en tredimensionel geometrisk form, der består af en cylinder og to halvkugleformede ender, hvor en halvkugle er en halv kugle. Det følger heraf, at rumfanget af en kapsel kan beregnes ved at kombinere ligningerne for en kugle og en ret cirkulær cylinder:

Rumfanget af en kapsel = π * r^2 * h + 4/3 * π * r^3 = π * r^2(4/3 * r + h)

hvor r er radius og h er højden af den cylindriske del

Keglestub

En keglestub er den del af et fast stof, der bliver tilbage, når en kegle skæres af to parallelle planer. Denne lommeregner beregner rumfang for en højre cirkulær kegle specifikt. Typiske koniske frustums, der findes i hverdagen, omfatter lampeskærme, spande og nogle drikkeglas. Rumfanget af en ret konisk stum beregnes ved hjælp af følgende ligning:

Rumfang af en kuglestub = 1/3 * π * h (r^2 + r * R + R^2)

hvor r og R er radierne af baserne, h er højden af stubben

Elipsoide

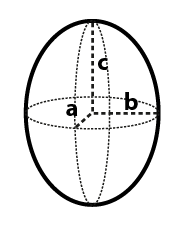
En ellipsoide er det tredimensionelle modstykke til en ellipse, og er en overflade, der kan beskrives som deformation af en kugle gennem skalering af retningsbestemte elementer. Centrum af en ellipsoide er det punkt, hvor tre parvis vinkelrette symmetriakser skærer hinanden, og linjestykkerne, der afgrænser disse symmetriakser, kaldes hovedakserne. Hvis alle tre har forskellige længder, beskrives ellipsoiden almindeligvis som treaksial. Ligningen for at beregne volumenet af en ellipsoide er som følger:

Rumfang af en elipsoide = 4/3 * π * a * b * c

hvor a, b og c er længderne af akserne

Pyramide

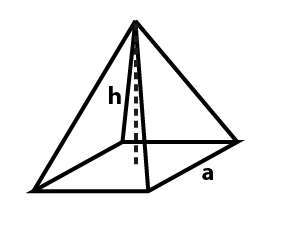
En pyramide i geometri er et tredimensionelt fast stof dannet ved at forbinde en polygonal base til et punkt kaldet dens toppunkt, hvor en polygon er en form i et plan afgrænset af et begrænset antal lige linjestykker. Der er mange mulige polygonale baser for en pyramide, men en firkantet pyramide er en pyramide, hvor bunden er en firkant. En anden sondring, der involverer pyramider, involverer placeringen af spidsen. En højre pyramide har en top, der er direkte over tyngdepunktet af dens base. Uanset hvor spidsen af pyramiden er, så længe dens højde måles som den vinkelrette afstand fra planet, der indeholder basen til spidsen, kan pyramidens rumfang skrives som:

Generaliseret pyramiderumfang = 1/3 * b * h

hvor b er arealet af basen og h er højden

Kvadratisk pyramiderumfang = 1/3 * a^2 * h

hvor a er længden af basens kant

Rør

Et rør er en hul cylinder, der ofte bruges til at overføre væsker eller gas. Beregning af volumenet af et rør involverer i det væsentlige den samme formel som en cylinder (volumen=p*r^2*h), bortset fra at i dette tilfælde bruges diameteren i stedet for radius, og længden bruges i stedet for højden. Formlen involverer derfor måling af diameteren af den indre og ydre cylinder, som vist i figuren ovenfor, beregning af hver af deres volumener og subtrahering af rumfang af den indre cylinder fra den ydre. I betragtning af brugen af længde og diameter nævnt ovenfor er formlen til beregning af rumfanget af et rør vist nedenfor:

Rumfang af et rør = π * ((d1^2 – d2^2) / (4)) * l

hvor d1 er den ydre diameter, d2 er den indre diameter, og l er længden af røret

Vi håber du kunne bruge dette tekniske indlæg til dine beregninger.

Skriv gerne en kommentar hvis du har spørgsmål eller andet.

Hvis du gerne vil være mere om matematik kan du udforske vores blog vedrørende Matematik lige her!